Aprende en casa 2. Matemáticas. Primero de secundaria, 17 de septiembre.

 ¿DEBO O TENGO? ESE ES EL DILEMA.

APRENDIZAJE ESPERADO

Resuelve problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos.

ÉNFASIS

Operar con número enteros. Reglas de los signos.

Hemos visto que los números enteros se componen con los naturales (1, 2, 3,...), sus negativos y el cero. También sabemos que el valor absoluto de un número es su distancia al cero y que para saber cuál de dos enteros tiene mayor valor absoluto, sin importar que signo tengan, los hacemos positivos y tomamos el mayor. Por ejemplo, entre $-9$ y $3$, el de mayor valor absoluto es el $-9$ porque al hacerlo positivo vemos que $9$ es mayor que $3$.

Para sumar enteros, vamos a considerar que un número positivo indica que tenemos algo y un número negativo, que debemos esa misma cosa (que podría ser dinero). Vamos a considerar la suma de números enteros como una diversas combinaciones de deber y tener. Hay cuatro opciones:

• Dos deudas dan otra deuda. Al sumar dos negativos obtenemos otro negativo.

Si debo $7$ en un lado y debo $5$ en ootro, en total debo $12$. Esto se representa:

$$\left ( -7 \right ) + \left ( -5 \right )=-12$$

• Si tengo en un lado y tengo en otro, simplemente tengo. La suma de dos positivos es positivo.

Si tengo $\$15$ en una bolsa y $\$8$ en la otra, en total tengo $\$23$. Esto se puede escribir:

$$\left ( +15 \right ) + \left ( +8 \right )=+23$$

El signo positivo se puede omitir y se entiende que el número es positivo si no tiene signo inmediatamente a su izquierda.

$$\left ( 15 \right ) + \left ( 8 \right )=23$$ 

De aqui concluimos que al sumar dos números con el mismo signo, se suman los valores absolutos y el resultado conserva el signo.

• Si debo y tengo, pero debo más de lo que tengo, sigo con deuda pero más pequeña. Si el valor absoluto del número negativo es mayor que el positivo, al sumarse obtengo un número negativo con menor valor absoluto.

Si debo $12$ y tengo $4$, doy esos $4$ y mi deuda queda en $8$. En forma aritmética:

$$\left ( -12 \right ) + \left ( 4 \right )=-8$$

Si tengo $3$ y debo $8$, doy los tres y sigo debiendo $5$.

$$\left ( 3 \right ) + \left ( -8 \right )=-5$$

• Si debo y tengo, pero tengo más de lo que debo, sigo teniendo pero menos de lo que tenía. Si el número positivo es mayor que el valor absoluto del negativo, al sumarse obtengo un positivo más pequeño.

Si debo $9$ y tengo $14$, pego mi deuda y ahora tengo $5$.

$$\left ( -9 \right ) + \left ( 14 \right )=5$$

Si tengo $19$ y debo $10$, pago y me quedo con $9$.

Por lo tanto al sumar enteros con distinto signo, al de mayor valor absoluto se le resta el de menor y el resultado lleva el signo del de mayor valor absoluto.

_________________________________________________________________________

Para practicar vamos a resolver las siguientes operaciones:

$$\bullet -3+\left ( +5 \right )=$$

Como tienen signo distinto se van a restar, el de mayor valor absoluto es el $+5$ (esta más lejos del cero que el $-3$), por lo tanto el resultado va a ser positivo:

 $$ -3+\left ( +5 \right )=+2$$

_________________________________________________________________________

$$\bullet  -3+\left ( -5 \right )=$$

Como tienen el mismo signo se suman los valores absolutos y el resultado mantiene el signo: 

$$ -3+\left ( -5 \right )=-8$$

________________________________________________________________________

$$\bullet  +3+\left ( +5 \right )=$$

Estos tambien tienen el mismo signo, se suman y el resultado se queda con el mismo signo: 

$$+3+\left ( +5 \right )=+8$$

________________________________________________________________________

$$\bullet  +3+\left ( -5 \right )=$$ 

Tienen signo distinto, se restan y como el de mayor valor absoluto es el $-5$, el resultado será negativo:

$$\bullet  +3+\left ( -5 \right )=-2$$ 

________________________________________________________________________

Una forma de visualizar esto es representando a los negativos con círculos rojos y a los positivos con azules. sabemos que si debo $7$ y tengo $7$, pago y me quedo sin nada, es decir:

$$\left ( -7 \right ) + \left ( 7 \right )= 0$$

Y en general si lo que tengo es igual a lo que debo me quedo sin nada. Por lo tanto, cantidades iguales de círculos rojos y azules, representan al cero. Ejemplos:

$$\left ( -1 \right ) + \left ( 1 \right )= 0$$

 

 

$$\left ( 4 \right ) + \left ( -4 \right )= 0$$

 

Esto significa que los círculos emparejados se anulan para dar cero.

Para sumar $\left ( +4 \right )+\left ( -6 \right )$ ponemos 4 círculos azules y 7 rojos.

Pero:

Los emparejados se anulan:

 

Nos quedan dos rojo (negativos), por lo tanto

$$\left ( +4 \right )+\left ( -6\right )=-2$$

Un último ejemplo:

¿Cuál es el resultado de sumar $\left ( -2 \right )+\left ( +5 \right )$.

 Necesitamos tres círculos rojos y 5 azules.

 

Eliminamos las que se emaparejan:

Por lo tanto nos queda:

El resultado son tres círculos azules, es decir: $+3$. En otras palabras:

$$\left ( -2 \right )\left (+5  \right )=+3$$

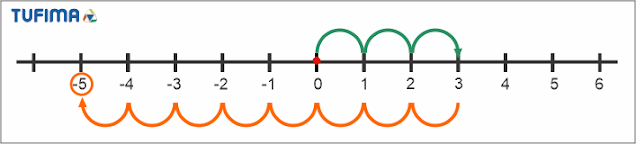
Otra forma de hacer estas operaciones es con la recta numérica, comenzamos del cero, el signo positivo indica movimiento hacia la derecha y el negativo hacia la izquierda. El número nos dice cuántos espacios movernos. Por ejemplo 

$$3-8$$

Comenzamos en el cero.

Nos movemos tres unidades a la derecha.

Y de aquí, ocho hacia la izquierda.

Por lo tanto:

$$3-8=-5$$

Con esto terminamos.