Aprende en casa 2. Matemáticas. Tercero de secundaria, 16 de septiembre.

 RESOLUCIÓN DE ECUACIONES DE SEGUNDO GRADO DE LA FORMA $ax^{2}+c=0$ DESPEJANDO LA INCÓGNITA.

APRENDIZAJE ESPERADO

Resuelve problemas que implican el uso de ecuaciones de segundo grado.

ÉNFASIS

Resolver problemas que implican el uso de ecuaciones de segundo grado a través de procedimientos formales.

En ocasiones es necesario realizar operaciones algebraicas para econtrar la ecuación cuadrática que vamos a resolver. Las operaciones que nos llevan a ecuaciones de la forma $ax^{2}+c=0$ son:

• Producto de monomios del tipo $\left ( ax \right )\left ( bx\right )$ y el resultado es $abx^{2}$ donde $ab$ significa  $a$ por $b$. Ejemplos:

$$\left ( 3x \right )\left ( 7x \right )=21x^{2}$$

En este caso $a=3$ y $b=7$ y $3$ por $7$ es $21$

  $$\left ( x \right )\left ( 9x \right )=9x^{2}$$

En este caso $a=1$ y $b=9$ y $1$ por $9$ es $9$

$$\left ( -4x \right )\left (  5x\right )=-20x^{2}$$

Ya que $-4$ por $5$ es $-20$

• Producto de binomios conjugados que son de la forma $\left ( x+a \right )\left ( x-a \right )$ (la incógnita más un número por la incógnita menos el mismo número) el resultado es $x^{2}-a^{2}$.

Ejemplos:

$$\left ( x+7\right )\left ( x-7 \right )=x^{2}-7^{2}=x^{2}-49$$

Nótese que $a$ tiene el valor de $7$.

$$\left ( x-2\right )\left ( x+2 \right )=x^{2}-2^{2}=x^{2}-4$$

El orden de los factores no altera el producto, por lo tanto si aparece primero $\left ( x-2\right )$ el resultado es el mismo. En este ejemplo el valor de $a$ es $2$.

• Producto como $a\left ( bx^{2}+c\right )$, aquí el número que está fuera del paréntesis multiplica a los que están dentro, dando como resultado $abx^{2}+ac$.

Ejemplos:

$$5\left ( 6x^{2}+3\right )=30x^{2}+15$$

El $5$ multiplicó al $6$ y al $3$.

$$8\left ( 4x^{2}-7\right )=32x^{2}-56$$

El $8$ multiplicó al $4$ y al $7$.

Un caso especial de este producto es cuando en  $\left ( bx^{2}+c\right )$, $c=0$. Como en el siguiente ejemplo:

$$9\left ( 3x^{2}\right )=27x^{2}$$

 Ahora vamos a resolver algunos ejercicios de ecuaciones cuadráticas:

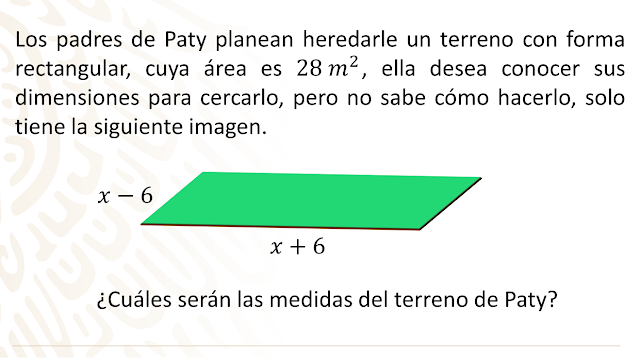
El área de un rectángulo se obtiene multiplicando las longitudes de sus lados, en este caso $\left (x+6  \right )\left ( x-6 \right )$ se trata de un producto de binomios conjugados y ya vimos como multiplicarlos

$$\left (x+6  \right )\left ( x-6 \right )=x^{2}-36$$

Como sabemos que esta área es de $28 m^{2}$, tenemos la ecuación:

$$x^{2}-36=28$$

La podemos resolver aplicando operaciones inversas (como vimos en las entradas anteriores): 

$$x^{2}=28+36=64$$

$$x=\sqrt{64}=8$$

Como $x=8$ las longitudes de los lados son:

$$x-6=8-6=2$$

$$x+6=8+6=14$$

 

 

 

El área del rectángulo es el producto de sus lados por lo tanto tenemos la ecuación:

$$\left ( x \right )\left (  2x\right )=5000$$

$$\left ( 2x^{2} \right )=5000$$

La resolvemos utilizando operaciones inversas:

$$x^{2}=\frac{5000}{2}=2500$$

$$x=\sqrt{2500}=50$$

El valor de $x$ es 50, por lo tanto un lado mido $50m$ y el otro el doble, $100m$.

El área del cuadrado es lado por lado o lado al cuadrado.

Por lo tanto tenemos la ecuación:

$$x^{2}=36$$

Que se resuelve fácilmente.

$$x=\sqrt{36}=6$$

El lado mide $6m$.