Aprende en casa 2. Matemáticas. Primero de secundaria, 18 de septiembre.

 

 JUEGA CON ACTITUD POSITIVA..¿O NEGATIVA?

APRENDIZAJE ESPERADO

Resuelve problemas de suma y resta con números, fracciones y decimales positivos y negativos.

ÉNFASIS

Restar números con signo.

Esta entrada será breve, nos enfocaremos a restar números enteros y utilizaremos un procedimiento bastante sencillo. Pero antes vamos explicar un concepto clave: el inverso aditivo.

Se llama inverso aditivo de un número a su simétrico respecto al cero. Esto implica que tienen el mismo valor absoluto, pero difieren en el signo.

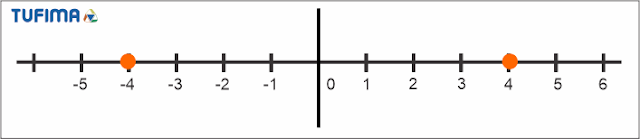
Como se puede observar en la siguiente imagen:


El simetrico de $4$ es $-4$ y viceversa, también se dice que el $4$ es el inverso aditivo del $-4$ y viceversa.

Ahora podemos pasar a la resta entre entero, vamos a ponerlo así:

Si a un entero le restamos otro, el resultado es igual, si al mismo entero le sumamos el inverso aditivo de la cantidad restada. Esto nos permite, transformar la resta en una suma y poder utilizar los métodos de la entrada anterior. Esto significa que en lugar de:

$$\left ( -4 \right )-\left ( -7 \right )$$

Podemos resolver:

$$\left ( -4 \right )+\left ( +7 \right )$$

Y da lo mismo. Restar $-7$ es lo mismo que sumar el inverso aditivo de $-7$ que es $+7$.

Otro ejemplo, para no restar:

$$\left ( +8 \right ) - \left ( +5 \right )$$

Convertimos la operación en una suma, utilizando el inverso aditivo de $+5$:

$$\left ( +8 \right ) + \left ( -5 \right )$$.

Para finalizar vamos a resolver algunos ejemplos.

1.- ¿Cuál es el resultado de $-4- \left ( +9 \right )$?

El inverso aditivo (o simétrico) de $+9$ es $-9$ entonces en lugar de restar vamos a sumar esta cantidad. La operación queda:

$$-4+ \left ( -9 \right )$$

Vimos tres métodos para hacer esta suma, vamos a utilizar el de deber y tener. Si debo $4$ en un lado y debo $9$ en otro en total debo $13$, por lo cual: 

$$-4-+ \left ( -9 \right )=-13$$

1.- ¿Cuál es el resultado de $8- \left ( +10 \right )$?

Con el inverso aditivo de $+10$ transformamos la resta en suma.

$$8+ \left ( -10 \right )$$ 

Y si tengo $8$ pero debo $10$ pago los $8$ y sigo debiendo $2$. Es decir:

$$8+ \left ( -10 \right )= -2$$

Comentarios

Publicar un comentario

Entradas populares de este blog

Teselados I

Imagen
En su versión más simple, teselar significa cubrir una superficie (también puede ser el espacio pero de eso hablaremos después) con elementos regulares o irregulares, sin dejar resquicios y sin sobreponerse. A un arreglo de formas bidimensionales que cumplan esas características se le llama teselado y se puede clasificar de la siguiente manera: Teselados Periódicos    Son aquellos que tienen traslaciones que los hacen coincidir con ellos mismos. Tenemos los siguientes casos: Teselados Regulares: El plano se cubre con un solo tipo de polígono regular (los que tienen lados y ángulos iguales). Teselado Semirregular: Este cubrimiento contiene más de un polígono regular, con la condiciòn de que el arreglo de polígonos sea el mismo en cada vértice. Teselado Demirregular: Utiliza más de un polígono regular como en el caso anterior pero el patrón no se repite en cada vértice. Teselado Irregular: Es el que no contiene polígonos regulares. Teselados Aperiódicos  S
Leer más

Área del trapecio.

Imagen
Uno de los errores más comunes en la enseñanza de las matemáticas, es proporcionar a los estudiantes contenidos ya digeridos, evitando el proceso que permite asimilar de manera más aficaz los conceptos.  La abismal diferencia entre las matemáticas reales y la pálida y cutre asignatura que se imparte en las escuelas se vuelve más evidente al contemplar  el manejo que se le da a la geometría. Cabe recordar que esta fue una de las primeras construcciones lógicas, el primer edificio solidamente cimentado en una estructura axiomática y donde cada afirmación descanza en una serie de argumentos y procedimientos que demuestran su veracidad. A pesar de esto, lo que llega a las aulas es un conjunto de fórmulas que nadie sabe de dónde vienen pero que hay que memorizar y aplicar. Ya tendremos tiempo de profundizar en esto, ahora vamos a presentar diversas maneras de obtener la fórmula del área de un trapecio. Para ponernos al día, un trapecio es un cuadrilatero convexo que tiene paralelos
Leer más

Aprende en casa 2. Matemáticas. Primero de secundaria, 8 de septiembre.

Imagen
ARISTAS, CARAS Y VÉRTICES Aprendizaje esperado  Construcción de cuerpos geométricos con distintos materiales (incluyendo cono, cilindro y esfera). Análisis de sus características referentes a la forma y al número de caras, vértices y aristas. Las figuras geométricas se pueden clasificar por sus dimensiones. Las figuras planas están limitadas por líneas rectas y curvas, tienen 2 dimensiones, largo y ancho y no tienen volumen, solo superficie. Algunos ejemplos son:   Los cuerpos gemétricos están limitados por superficies planas o curvas, tienen tres dimensiones y por supuesto volumen. Estas figuras tridimensionales tienen los siguientes elementos: Caras: son las superficies que la limitan, pueden ser rectas como en el cubo o curvas como en el cilindro. Aristas: son las intersecciones entre dos caras, pueden ser rectas como en las pramides o curvas como en el cono. Vertices: son puntos donde se juntas dos a más aristas. Como ejemplo de figuras tridimensionales tenemos: Prismas Un prisma e
Leer más