Aprende en casa 2. Matemáticas. Segundo de secundaria, 8 de septiembre.

LO QUE APRENDAS HOY SERÁ DIRECTAMENTE PROPORCIONAL A LA ATENCIÓN QUE PONGAS

Aprendizaje esperado

Calcula valores faltantes en problemas de proporcionalidad directa, con constante natural, fracción o decimal (incluyendo tablas de variación).

La proporcionalidad directa y tiene las siguientes características:

1. Las variables crecen o disminuyen en la misma proporción. Si una de ellas se triplica la otra cambia igual y si una de ellas se reduce a la mitad, la otra también.
2. Las dos variables son cero al mismo tiempo, es decir, si una de ellas es cero, la otra también.
3. Al dividir una entre la otra siempre obtenemos la misma cantidad que se conoce como constante de proporcionalidad y es el número por el que multiplicamos a la $x$ para obtener la $y$.
   

Estas  propiedades nos permiten identificar si una tabla de variación es es una proporcionalidad directa.

Esta tabla de variación no es de proporción directa porque cuando la $x$ es cero, la $y$ no y en este tipo de proporcionalidad ambas deben ser cero al mismo tiempo.

 

 

Este tabla tampoco representa una relación de proporcionalidad directa, porque al dividir cada valor de $y$ entre su respectivo valor de $x$ no obtenemos lo mismo.

                             

Esta si es de proporción directa, lo podemos ver de dos formas: la primera al darnos cuenta que al dividir cada valor de $y$ entre su correspondiente valor de $x$ siempre obtenemos 6 y la segunda porque al duplicar el valor de $x$ se duplica el de $y$, al doble de 3 que es 6. le corresponde el doble de 18, que es 36. Ademas al tripli de 2, que es 6, le corresponde el triple de 12 que es 36.

Con esto vamos resolver los ejercicios planteados en la lección.

1. El momento en que se ve un rayo, se considera igual al momento en que cae, pero el sonido llega unos segundos después. Manuel midió con un cronométro 4s entre la luz de un rayo y el sonido del estruendo y dice que el rayo cayó 1372 m de distancia del lugar donde el se encontraba. ¿Cómo podemos construir una tabla de variación proporcional directa con los datos que se muestran en la siguiente tabla?

Como es una proporción directa al ser 2,  la mitad de 4, la distancia para  2 segundos es la mitad de 1372, es decir 686.

 También podemos encontrar la constante de proporcionalidad dividiendo un valor de $y$ entre su respectivo valor de $x$, por ejemplo:

$$\frac{1372}{4}=343$$

Entonces basta multiplicar cada valor del tiempo por esta cantidad:

$$(3.6)(343)= 1234.8$$

$$(5.4)(343)=1852.2$$

Con esto la tabla nos queda:

Esto nos da una manera de calcular la distancia a la que cayó un rayo, cuando veamos la luz contamos hasta escuchar el estruendo, los segundo que pasen en ese lapso se multiplican por 343 y obtenemos la distancia de donde estamos hasta donde cayó el rayo.

2.-  En la escuela se inició una campaña de recolección de material reciclable para venderlo y obtener fondos para el programa de becas. Para vender el papel recopilado se buscó en internet información para elaborar las siguientes tablas de proporcionalidad directa:

¿En cuál de las tres recicladoras ganaremos más al vender el papel blanco?

Como sabemos que se trata de tablas de proporcionalidad directa, lo que podemos hacer es buscar la constante de proporcionalidad de cada una de ellas, esta constante representa la cantidad que nos pagarán por cada kilogramos de papel:

En Recicla todo:

$$\frac{1,50}{0.5}=3$$

En Mundo verde:

$$\frac{4.80}{1.5}=3.2$$

En Planeta limpio:

$$\frac{8.10}{2.25}=3.6$$

por lo tanto nos conviene más llevar nuestro papel a Planeta limpio ahí nos pagarán más ($3.6 por cada kilo) que en las otras recicladoras.

Otra de resolver problemas de valores faltantes en relaciones de proporcionalidad directa es con la regla de tres, para ver como funciona reslveremos el siguiente ejercicio:

3.- Si 40 vacas consumen 4200 kg de forraje, ¿cuánto forraje consumirán 13 vacas? 

Para poder utilizar la regla de tres primero nos cercioramos de que estamos trabajando con una proporción durecta. Esto es fácil, basta observar que cero vacas comen cero kilogramos de forraje (ambas variables son cero al mismo tiempo) y si duplicamos el número de vacas se duplica la cantidad de forraje. 

Una vez hecho esto vamos a la regla de tres, esta se basa en la propiedad de la proporción directa de dar siempre lo mismo al dividir las variables correspondientes. Vamos a dividir los kilogramos entre el número de vacas, para esto llamamos $y$ a los kilogramos que corresponden a 13 vacas:

$$\frac{4200}{40}=\frac{y}{13}$$

 La variable desconocida se encuentra multiplicando en diagonal los valores conocidos y dividiendo el resultado entre el dato que no hemos utilizado:

$$y=\frac{(13)(4200)}{40}=\frac{54600}{40}=1365$$

4.- Un arbol mide 8.4 m de altura y a cierta hora del día proyecta una sombra de 11.2 m de longitud. ¿Cuál será la altura de Juan si a la misma hora del día proyecta una sombra de 2 m de longitud. La relación entre la altura y la sobra es de proporción directa, si se triplica la altura, se triplica la sombra. 

Por lo tanto utilizaremos la regla de tres:

Dividiremos la altura entre la sombra, para la altura correspondiente a 2 m de sombra utilizaremos la variable $y$:

$$\frac{8.4}{11.2}=\frac{y}{2}$$

Para despejar la $y$ se multiplica cruzado $(2)(8.4)$ y se divide el resultado entre $11.2$.

$$y=\frac{(2)(8.4)}{11.2}=\frac{16.8}{11.2}=1.5$$

Juan mide 1.5 m. 

Otra forma de representar la proporcionalidad directa es mediante una gráfica. La proporcionalidad directa se grafica con una línea recta que pasa por el origen.

Para ver como trabajar con ellas resolveremos el siguiente ejemplo:

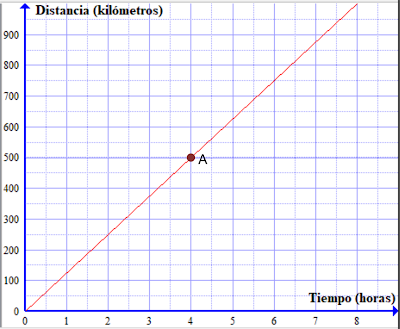
5.- La siguiente gráfica muestra la relación proporcional entre la distancia que recorre un tren y la cantidad de tiempo que le toma recorrerla.

 

¿Cuáles propocisiones sobre la gráfica son verdaderas?

• La coordenada vertical del punto A representa la distancia total que recorre el tren en 500 minutos.

Esta es falsa lo que el punto A indica es que el tren recorre 500 km en 4 horas

• El tren recorre 375 km en 3 horas.

Para ver si esto es cierto vamos  a encontrar la constante de proporcionalidad, sabemos que esta se encuentra dividiendo las variables, como en 4 horas, recorre 500 km:

$$\frac{500}{4}=125$$

Esto nos da la velocidad a la que viaja el tren 125  $\frac{km}{h}$. Por lo tanto basta multiplicar:

$$(3)(125)=375$$

De aquí vemos que esta opción si es correcta. 

6.- La gráfica muestra el tiempo necesario para instalar cercado de diferente longitud.

¿Cuáles propocisiones sobre la gráfica son verdaderas?

• El punto$(2,30)$ muestra que el costo es de $30 por 2 m de cercado.
• El punto $(4,60)$ muestra que toma 4 horas instalar 60 m de cercado.

Antes de ver cuál es verdadera, hay que mencionar que la gráfica al ser recta y pasar por el origen, es una relación de proporcionalidad directa. Esta gráfica relaciona la longitud de un cerco con el tiempo que se tarda en hacerlo, por lo tanto no da información sobre los costos, esto hace que la primera opción sea falsa. La segunda es verdadera. Para encontrar la relación entre tiempo y longitud, ubicamos la hora que nos interesa, de ahí avanzamos verticalmente hacia arriba hasta encontrar la recta, despues nos movemos horizontalmente hacia la izquierda hasta encontrar el eje vertical para encontrar la longitud correpondiente.

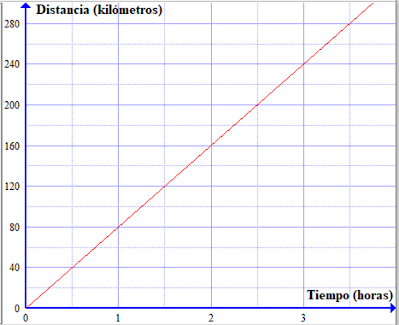
7.- Un automovil viaja por una carretera a la rapidez constante que se muestra en la gráfica. Encuentra la rapidez del auto.

Para encontrar la velocidad necesitamos relacionar el tiempo con su respectiva distancia, para esto procedemos como como lo mencionamos en el ejercicio anterior. Nos vamos a ubicar en 2 horas y subimos, al llegar a la recta nos desplazamos hacia la izquierda:

Nos encontramos con el 160, esto significa que el auto recorre 160 km en 2 h por lo tanto su velocidad es:

$$\frac{160km}{2h}=80\frac{km}{h}$$