Aprende en casa 2. Matemáticas. Segundo de secundaria, 17 de septiembre.

FACTOR DE ESCALA Y EL FACTOR INVERSO DE ESCALA. EL RECÍPROCO

APRENDIZAJE ESPERADO

Resuelve problemas de multiplicación y división con fracciones y decimales positivos

ÉNFASIS

Aplicar los factores de escala.

Recíproco

Cada número tiene asociado otro llamado recíproco. Con la característica de que al multiplicar cualquier cantidad por su recíproco obtenemos uno. esto nos dá una técnica para encontrar el recíproco de cualquier número. Ejemplo: 

1.-¿Cuál es el recíproco de 8? 

Llamamos al recíproco $x$, por lo tanto:

$$8x= 1$$

Ya que el producto de cualquier número por su recíproco es igual a uno:

Por lo tanto, despejamos:

$$x=\frac{1}{8}$$

2.- ¿Cuál es el recíproco de $\frac{3}{5}$?

Si el recíproco es $a$, tenemos la ecuación:

$$\left ( \frac{3}{5} \right )\left ( a \right )=1$$

$$a=\frac{5}{3}$$

El tres que estaba multiplicando pasa dividiendo y el cinco que estaba dividiendo pasa multiplicando.

Podemos observar que si $n$ es un número entero $\frac{1}{n}$ es el recíproco.

Y el recíproco de la fracción $\frac{a}{b}$ es $\frac{b}{a}$

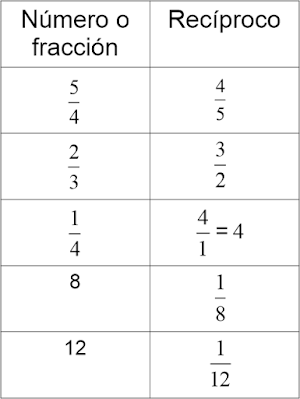
En la siguiente tabla se nuestran algunos números y fracciones con sus respectivos recíprocos.

 

Ahora si estamos listos para trabajar con los factores de escala.

Factor de escala y su recíproco.

Se dice que dos figuras están a escala cuando las dimensiones de una de ella se obtienen multiplicando por una misma cantidad las dimensiones correspondientes de la otra.

Los trapecios de la figura están a escala, la altura y los lados del más grande se obtienen multiplicando por tres los correspondientes de la más chica. Esto significa que el factor de escala es 3. Una forma de representarlo es: $1:3$ que nos dice que por cada centímetro de uno hay tres del otro.

Para ver cómo encontrar el factor de escala, tenemos el siguiente ejemplo:

Si los trapecios mostrados son semejantes, ¿cuál es el factor de escala? Encontrar el valor de las magnitudes que faltan.

Para resolverlo vemos que el lado correspondiente al de 8cm mide 12cm, entonces nos preguntamos: ¿por cuánto hay que multiplicar al 8 para que dé 12? Podemos hacer una ecuación, donde $x$ es el factor de escala:

$$8x=12$$

Que nos da:

$$x=\frac{12}{8}=1.5$$

El factor de escala es 1.5. Por lo tanto, para encontrar las magnitudes que faltan hay que multiplicar las correspondientes del pequeño por 1.5.

$$L=(6)(1.5)=9cm$$

$$b=(5)(1.5)=7.5cm$$

$$h=(5.8)(1.5)=8.7cm$$

3.- Encontrar el factor de escala en la siguiente figura y los valores faltantes.

Para encontrar el factor de escala se requiere conocer los valores de por lo menos un par de lados correspondientes y la figura nos los da. El lado correspondiente al de de 16 cm mide 20cm.

Nos preguntamos ¿por cuánto multiplicamos al 16 para que nos de 20? Por $x$, entonces:

$$16x=20$$

$$x=\frac{20}{16}= \frac{20\div 4}{16\div 4}=\frac{5}{4}$$

El factor de escala es $\frac{5}{4}$ 

Las medidas de la figura más grande se encuentras multiplicando la de las pequeñas por $\frac{5}{4}$

El lado correspondiente al de $7cm$ es:

$$\left ( 7 \right )\left ( \frac{5}{4} \right )=\frac{35}{4}$$

El lado que corresponde al de $10cm$ es:

$$\left (10 \right )\left ( \frac{5}{4} \right )=\frac{50}{4}$$

Por lo tanto:

 

O en decimales:

Si para trazar una figura a partir de otra se utiliza un factor de escala $k$ para volver a la original el factor de escala es el recíproco del que se utilizó:

Esto significa que si:

Entonces:

En el ejercicio 5, como el factor de escala es $\frac{5}{4}$ para pasar de la figura grande a la pequeña será el recíproco, es decir, $\frac{4}{5}$

Es seguro que si multiplicamos $20$ por $\frac{4}{5}$ obtenemos $16$.

Si hay una serie de figuras a escala, para pasar de una a otra se utiliza un factor de escala igual al producto de los factores de las figuras intermedia, esto se explica en la siguiente imagen.

Aquí se ve que si el factor de escala de una figura a otra es $k$, el factor para regresar a la primer figura es el recíproco.

Por último vamos a resolver un ejercicio:

4.- Encontra la longitud de los segmentos $\overline{C'D'}$ y $\overline{C''D''}$ (de las figuras 2 y 3) y los segmentos $\overline{EF}$ y $\overline{E'F'}$ (de las figuras 1 y 2).

Se puede observar facilmente que el factor de escala de la figura 1 a la 2 es $2$ porque al multiplicar la base de $4cm$ por $2$ obtenemos la base de la segunda que es $8cm$.

Entonces para encontrar $\overline{C'D'}$, basta multiplicar la longitud de $\overline{CD}$ por dos. Por lo tanto:

$$\overline{C'D'}=4cm$$

Para encontrar el factor de escala de la segunda a la tercera nos preguntamos: ¿por cuánto multiplicamos al 8 para que nos de 12? Como no sabemos le llamamos $x$ y hacemos una ecuación:

$$8x=12$$

$$x=\frac{12}{8}=\frac{12\div 4}{8\div 4}=\frac{3}{2}$$  

Para pasar de la segunda a la tercera el factor es $\frac{3}{2}$.

 

Por lo tanto para encontrar $\overline{C''D''}$ hay que multiplicar $\overline{C'D'}$ por $\frac{3}{2}$.

$$\left ( 4 \right )\left ( \frac{3}{2} \right )=\left ( \frac{4}{1} \right )\left ( \frac{3}{2} \right )=\frac{12}{2}=6$$

$$\overline{C''D''}=6cm$$

Si quisieramos pasar de la figura 1 a la 3, el factor es el producto de los factores intermedios.

$$\left ( 2 \right )\left ( \frac{3}{2} \right )=\left ( \frac{2}{1} \right )\left ( \frac{3}{2} \right )=\frac{6}{2}=3$$

 

El factor de escala para pasar de la 1 a la 3,  es $3$, esto quiere decir que para encontrar $\overline{C''D''}$ también pudimos haber multiplicado $\overline{CD}$ por $3$.

$$\left ( 2 \right ) \left ( 3 \right )= 6cm$$

Para encontrar  $\overline{EF}$ y $\overline{E'F'}$ vamos a utilizar $\overline{E''F''}=9cm$ y los recíprocos de los factores de escala.

Para encontrar $\overline{E'F'}$ se multiplica $\overline{E''F''}$ por $\frac{2}{3}$

$$\overline{E'F'}=\left ( 9 \right )\left ( \frac{2}{3} \right )=\frac{18}{3}=6cm$$

Para encontrar  $\overline{EF}$ tenemos dos opciones, multiplicar $\overline{E''F''}$ por $\frac{1}{3}$ o multiplicar $\overline{E'F'}$ por $\frac{1}{2}$, en ambos casos da lo mismo:

$$\overline{EF}=\left ( 9 \right )\left ( \frac{1}{3} \right )=\frac{9}{3}=3cm$$

$$\overline{EF}=\left ( 6 \right )\left ( \frac{1}{2} \right )=\frac{6}{2}=3cm$$

 Hemos terminado.